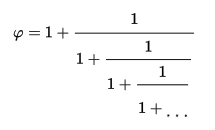Golden Waves
The theory behind the waves based on the golden number |
|
The golden number comes from the divine proportion that divides The whole into parts by an ideal ratio, so that every part will reflect the whole. The principle which is at the base of the universe in creates and sustains it. Mathematically the entire reported by a part must be equal to the ratio of the two divisions.
1/a = a/b 1/a = a/(1-a) 1=a*a+a
a=0,618033988....
|
Divine ratio is a perfect ratio which creates everything |
|
Thus we have obtained an ideal primary division. To keep this perfection we must continue in the same way, the obtained divisions we divide them by the golden ratio. This way you can get a perfect growth and division that maintains the holistic principle: the part in everything and everything in the part. This principle is also used in fractals.
Mathematically we can write: It is a growing and an indefinitely dividing formula that can grow infinite keeping the original harmony.
|
Non-linear time concept |
|
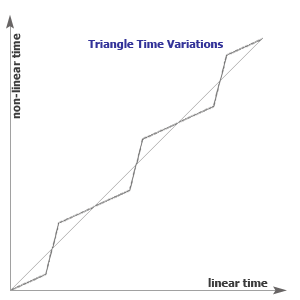
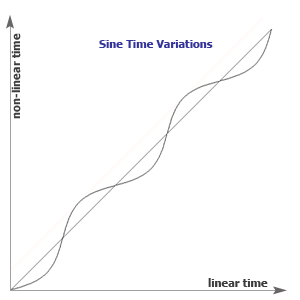
The symmetrical sinusoid (classic sinusoid) is based on a linear time but the time is non-linear! Golden sinusoid is based on a non-linear time, cyclical with a waveform variations too. So this is the way how we generate the Golden Sinusoid in our generators.
Time variations based on Golden Triangle Wave: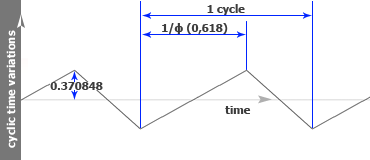
Time variations based on Sine Wave: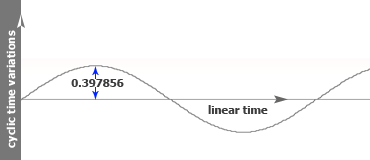
Time variations based on Sine Wave with Golden Number Amplitude: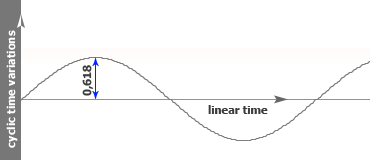
We have used two constants on amplitude which are amazingly very close to the golden number (more exactly, unit reduced by the golden number). |
Golden waveforms |
|
Golden Sinusoid TS:Using the non-linear time concept, we apply a triangle wave on the time axis and then generate a classical sinusoid. Mathematical is a Triangle wave in a Sine wave (TS). So we got a divided wave cycle in two perfect divisions through the golden ratio as follows: 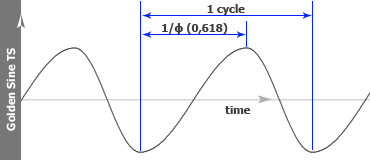
This wave was used on our precedent generators like: goldenSynth, binauralTones, isochronicTones, goldenGenerator and GoldenWavesGenerator
Golden Sinusoid SG:On this wave, we apply a sine wave on the time axis and then generate a classical sinusoid. Mathematical is a Sine wave in a Golden sine wave (SG). Final result it is amazingly a sine wave based on the number of gold as follows: 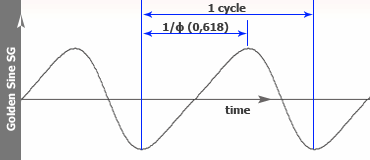
Golden Sinusoid GS:Finally, on the last sine we apply a sine wave with golden number on the variations time amplitude then generate a classical sinusoid. Mathematical is a Golden amplitude sine wave in a Sine wave (GS). This is the result: 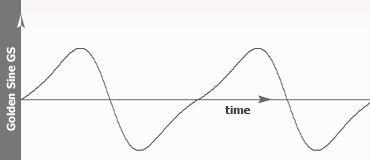
Golden Sinusoid SG and GS waves was used on the GoldenWavesGenerator generator.
Golden Triangle Wave:We start with the triangle golden wave because basis on its we generated the sine wave. 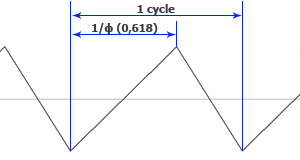
Golden Sine Half: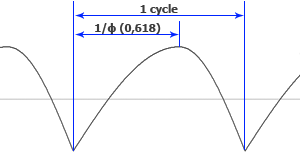
Golden Square Wave: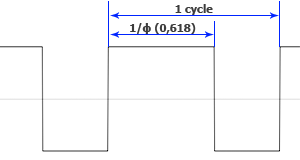
In this way we obtained pure, ideal waveforms, with a specific timbre, excellent for binaural beats. You can make a lot of therapeutic sounds, in a psychological or spiritual domain and you can add this tones to music, nature sound etc.
|
Golden waveforms - natural waves |
|
The perfectly symmetrical sinusoid does not exist in nature, the waves are inclined to propagate through an environment. The inclination depends on the permeability of the environment and the distance from the center of oscillation - but this is not part of our studies. If we take into account the nonlinearity of time, we get a better approximation of some waves in nature such as ocean waves and earth waves. 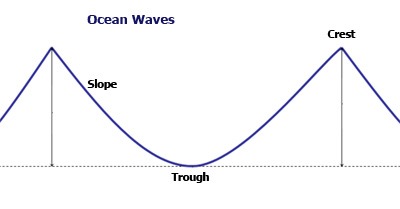 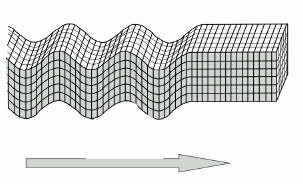 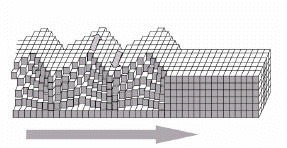 |
© Copyright |
|
This waveforms were discovered by EmRys, all rights regarding such wave shapes and concepts by: golden waveforms, golden sinusoid, golden triangle wave and golden square wave are exclusively reserved by © EmRys.
If you wish to use these waveforms for publication or post material that contains notions mentioned above it is absolutely necessary to specify the author's name and if the Internet is a medium for publication must add the website address http://www.emrys.ro/en or http://www.saschart.com
|